Najmniejszą liczbą całkowitą spełniającą nierówność $(3-x)(3+x)>(3-x)^2$ jest:
A. $0$
B. $1$
C. $2$
D. $3$
ROZWIĄZANIE:
Nierówność aż prosi się, żeby ją rozwiązać... Do dzieła!$$(3-x)(3+x)>(3-x)^2$$Na początek zastosujemy po lewej wzór skróconego mnożenia $(a-b)(a+b)=a^2-b^2$ a po prawej wzór $(a-b)^2=a^2-2ab+b^2$. Oczywiście można wszystko liczyć "na piechotę", ale po to mamy wzory, żeby je stosować:-)
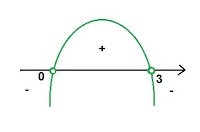
Nasza nierówność po zastosowaniu wzorów, prezentuje się następująco:$$9-x^2>9-6x+x^2$$Przenosimy wszystko na jedną stronę:$$9-x^2-9+6x-x^2>0$$Porządkujemy$$-2x^2+6x>0$$Mamy równanie kwadratowe, wyciągamy $x$ przed nawias $$x(-2x+6)>0$$Wyznaczamy miejsca zerowe paraboli:$$x=0\ \ \ \vee -2x+6=0$$$$x=0\ \ \ \vee -2x=-6$$$$x=0\ \ \ \vee x=3$$Ramiona są oczywiście zwrócone w dół, kółka na końcach przedziału otwarte:
ODPOWIEDŹ: B.
Zadanie domowe:Nasza nierówność po zastosowaniu wzorów, prezentuje się następująco:$$9-x^2>9-6x+x^2$$Przenosimy wszystko na jedną stronę:$$9-x^2-9+6x-x^2>0$$Porządkujemy$$-2x^2+6x>0$$Mamy równanie kwadratowe, wyciągamy $x$ przed nawias $$x(-2x+6)>0$$Wyznaczamy miejsca zerowe paraboli:$$x=0\ \ \ \vee -2x+6=0$$$$x=0\ \ \ \vee -2x=-6$$$$x=0\ \ \ \vee x=3$$Ramiona są oczywiście zwrócone w dół, kółka na końcach przedziału otwarte:
Potrzebujemy rozwiązania większego od zera, a więc odczytujemy plusy:$$x\in (0;3)$$
W zadaniu pytają nas o najmniejszą liczbę całkowitą, która spełnia nierówność - będzie to 1, ponieważ 0 nie należy do naszego przedziału.
Największą liczbą całkowitą spełniającą nierówność $(3-x)(3+x)\geq(3+x)^2$ jest:
A. $0$
B. $1$
C. $2$
D. $3$





A. ;)
OdpowiedzUsuń